Homepage > The first Hertzsprung-Russell diagram
The first Hertzsprung-Russell diagram

Karl Schwarzschild (left) and Ejnar Hertzsprung in front of the Göttingen Observatory building sometime in 1909. A nearly identical picture, taken obviously at the same occasion, is reproduced in John B. Hearnshaw's excellent history of stellar spectroscopy, The Analysis of Starlight, page 211. The Göttingen Observatory photo, courtesy Hartmut Grosser.
Until quite recently [the article was first published on my old website in April 2000], I though that the first published HR diagram
was constructed by Ejnar Hertzsprung for the stars of the Pleiades.
Already in 1908, when Hertzsprung (then still an amateur astronomer with
training in photochemistry) visited Karl Schwarzschild at Göttingen,
he brought with him a working version with photographic magnitudes
plotted against effective wavelengths. To determine the latter quantity,
nowadays replaced by spectral type or color index, Hertzsprung attached
a coarse diffraction grating before the objective so that an ordinary stellar
image on the photographic plate was accompanied by a very short first-order
spectrum on either side. The separation of the most intense parts of
these spectra then directly translated into the effective wavelength
of the star's light. However, this first Hertzsprung attempt to visualize the
relation between luminosities and colors of stars suffered from a systematic
error due to influence of the secondary spectrum of the objective. It was not
until 1911, when the satisfactory version of the diagram was presented (Publ.
Astrophys. Observ. Potsdam 22, 1, 1911) together with a color-magnitude
diagram for another winter cluster, the Hyades.
In the meantime, Hans Rosenberg (1879–1940) of Göttingen published
a most interesting article in Astronomische Nachrichten. It's dated
June 1910, but note that both Schwarzschild (who proposed the measurements)
and Hertzsprung left the observatory already in 1909. I learned about this unique material from
an authoritative account on the history of the HR diagram published by Axel V.
Nielsen (Centaurus 9, 219, 1969). Given my own troubles finding this journal (I am indebted to Jaromir
Kucera for providing me with a photocopy during his stay at the University of Konstanz), and considering the fact that
even here the Rosenberg article is noted only in a footnote (#46), I decided
to make it more accessible for anyone interested in history of stellar astrophysics.
On the Relation Between Brightness and Spectral Type in the Pleiades
[Astronomische Nachrichten #4445, Vol. 186, p. 71, 1910] (pdf, 310 kB)
[Translated by Jan Hollan, Nicholas Copernicus Observatory and Planetarium Brno]
Instigated by Mr. K. Schwarzschild, I have made some long spectral exposures
of the Pleiades. I used the Zeiss UV-prism camera with a prism of low
dispersion (1.9 mm from H_gamma to H_zeta). The goal was to make
the most accurate determination of the spectral type of stars in the Pleiades. To
achieve this, I relied on the fact that the most sensitive measure
of the continuous evolution of the spectral type is comparison of the calcium
lines K and H with those of hydrogen. I compared the K line with the
H_delta and H_zeta using a decimal method [1],
as used for brightness estimates of variable stars. The H line
could not be used for this purpose as it coincides with H_epsilon.
I compared neither the density of the lines nor their widths, but
a physiological blend of both effects, which I would call "prominence".
When one of the lines was not visible at all whereas the other was clearly
recognizable, I set the difference of their prominences to 10; when they
were equally conspicuous, the difference was set to 0. All values lying
in between were estimated in tenths of this scale and written down as in the
Argelander step method, so that e.g. H_delta 4 K would mean that for
the corresponding star the prominence of H_delta has been estimated as
four steps of the scale greater than the prominence of K. The frequent
estimate 9.5 means that the observer after repeated attempts remained
unsure if the fainter line was present or not.
The following table contains the results from the plate No. 688. That
plate had the sharpest spectra and its 90-minute exposure enabled
classification of spectral types up to 10th magnitude class (photographic). Altogether,
the difference of prominence of K and both hydrogen lines was estimated
three times for each star. The spectrum was observed through a microscope,
and the stars were observed in succession that was changed each time. The
observer did never know which star is under the microscope. In this way
it was made sure that the series of estimates were independent on each other.
From the three estimates of each star the mean was computed. The
deviations of the single estimates from their mean give the inner random
mean error of one estimate 0.41 steps of the scale, but it seems
that the mean error depends also on the estimated difference of prominences.
The following table contains the following columns: 1) the designation of
the star by Bessel, 2) the number according to Bonner Durchmusterung, 3)
and 4) the photographic [2] and the optical [3]
brightness, 5) and 6) the three comparisons of H_delta with
K and their mean, 7) and 8) the three comparisons of H_zeta with K
and their mean. The stars are arranged in order of decreasing photographic brightness.
Spectra of some stars, that must have been on the plate due to their brightness
(e.g. Bessel 30, 18, 15, 8), are covered by spectra of another stars, so
that they could not be examined.
| Bessel | BD | mpg | mvis | Comparisons | Mean | Comparisons | Mean |
| eta |
23°541 |
3.41 |
3.19 |
H_delta |
9.5 |
10 |
9 |
K |
9.50 |
H_zeta |
10 |
10 |
9 |
K |
9.67 |
| f |
23°557 |
4.05 |
3.92 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
| b |
23°507 |
4.07 |
3.96 |
» |
9 |
9.5 |
9 |
» |
9.17 |
» |
9 |
9.5 |
9 |
» |
9.17 |
| c |
23°516 |
4.28 |
4.21 |
» |
10 |
10 |
10 |
» |
10 |
» |
10 |
10 |
10 |
» |
10 |
| d |
23°522 |
4.53 |
4.48 |
» |
9.5 |
10 |
9.5 |
» |
9.67 |
» |
9.5 |
10 |
9.5 |
» |
9.67 |
| e |
24°547 |
4.55 |
4.57 |
» |
8 |
8.5 |
7.5 |
» |
8.00 |
» |
8 |
8.5 |
8 |
» |
8.17 |
| h |
23°558 |
5.33 |
5.38 |
» |
9.5 |
10 |
9.5 |
» |
9.67 |
» |
9.5 |
10 |
9.5 |
» |
9.67 |
| 28 |
22°563 |
5.72 |
5.84 |
» |
10 |
10 |
9.5 |
» |
9.83 |
» |
10 |
10 |
9.5 |
» |
9.83 |
| g |
23°505 |
5.74 |
5.82 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
| k |
24°553 |
6.04 |
6.17 |
» |
9.5 |
10 |
9.5 |
» |
9.67 |
» |
9.5 |
9.5 |
10 |
» |
9.67 |
| 34 |
23°563 |
6.33 |
6.51 |
» |
9.5 |
9.5 |
8 |
» |
9.00 |
» |
9.5 |
9.5 |
7 |
» |
8.67 |
| p |
23°536 |
6.59 |
6.68 |
» |
9 |
9.5 |
9 |
» |
9.17 |
» |
9 |
9.5 |
9 |
» |
9.17 |
| l |
24°556 |
6.61 |
6.75 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
| 32 |
23°561 |
6.76 |
7.01 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
| 38 |
23°569 |
6.97 |
7.10 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
| 12 |
24°562 |
7.02 |
7.15 |
» |
9.5 |
10 |
9.5 |
» |
9.67 |
» |
9.5 |
10 |
9.5 |
» |
9.67 |
| 24 |
23°540 |
7.06 |
7.18 |
» |
10 |
10 |
10 |
» |
10 |
» |
10 |
10 |
10 |
» |
10 |
| s |
23°556 |
7.11 |
6.72 |
K |
7 |
8 |
8 |
H_delta |
7.67 |
K |
5 |
6 |
6 |
H_zeta |
5.67 *) |
| 19 |
23°537 |
7.20 |
7.31 |
H_delta |
9 |
9 |
8.5 |
K |
8.83 |
H_zeta |
9 |
9 |
8.5 |
K |
8.83 |
| 29 |
23°553 |
7.27 |
7.23 |
» |
7 |
9 |
7.5 |
» |
7.83 |
» |
7 |
9 |
7.5 |
» |
7.83 |
| 4 |
23°512 |
7.45 |
7.53 |
» |
9.5 |
9 |
9 |
» |
9.17 |
» |
9.5 |
9 |
9 |
» |
9.17 |
| 22 |
23°538 |
7.45 |
7.53 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
» |
9.5 |
9.5 |
9.5 |
» |
9.50 |
| 10 |
23°523 |
7.61 |
7.63 |
» |
9 |
9 |
9 |
» |
9.00 |
» |
9 |
9 |
9 |
» |
9.00 |
| 39 |
24°578 |
7.75 |
7.78 |
» |
8 |
8 |
8.5 |
» |
8.17 |
» |
8 |
8 |
8.5 |
» |
8.17 |
| 17 |
23°535 |
7.77 |
7.24 |
K |
9.5 |
9 |
9.5 |
H_delta |
9.33 |
K |
8 |
8 |
9 |
H_zeta |
8.33 *) |
| 37 |
23°567 |
7.77 |
7.84 |
H_delta |
7 |
8 |
8 |
K |
7.67 |
H_zeta |
7 |
8 |
8 |
K |
7.67 |
| 31 |
23°560 |
7.77 |
7.82 |
» |
7 |
7.5 |
7 |
» |
7.17 |
» |
7 |
7.5 |
8 |
» |
7.50 |
| 20 |
24°566 |
8.04 |
7.99 |
» |
6 |
6 |
6 |
» |
6.00 |
» |
6 |
7 |
6 |
» |
6.33 |
| 23 |
23°539 |
8.07 |
8.05 |
» |
6.5 |
6 |
7 |
» |
6.50 |
» |
6 |
7 |
6 |
» |
6.33 |
| 7 |
23°517 |
8.18 |
8.12 |
» |
7 |
7 |
7 |
» |
7.00 |
» |
8 |
7 |
8 |
» |
7.67 |
| 33 |
23°562 |
8.27 |
8.31 |
» |
6 |
6 |
6 |
» |
6.00 |
» |
6 |
7 |
7 |
» |
6.67 |
| 9 |
23°520 |
8.36 |
8.29 |
» |
4 |
4 |
3 |
» |
3.67 |
» |
5 |
3 |
4 |
» |
4.00 |
| 1 |
23°510 |
8.41 |
8.33 |
» |
7 |
8 |
6 |
» |
7.00 |
» |
7 |
8 |
6 |
» |
7.00 |
| 13 |
23°528 |
8.73 |
8.65 |
» |
3 |
2 |
2 |
» |
2.33 |
» |
2 |
2 |
1 |
» |
1.67 |
| 27 |
23°549 |
8.77 |
8.53 |
» |
5 |
3 |
3 |
» |
3.67 |
» |
4 |
4 |
2 |
» |
3.33 |
| 21 |
24°567 |
9.00 |
9.05 |
» |
10 |
10 |
10 |
» |
10 |
» |
10 |
10 |
10 |
» |
10 *) |
| 2 |
24°550 |
9.05 |
8.85 |
» |
4 |
7 |
4 |
» |
5.00 |
» |
4 |
6 |
5 |
» |
5.00 |
| 36 |
23°565 |
9.30 |
9.44 |
» |
10 |
10 |
10 |
» |
10 |
» |
10 |
10 |
10 |
» |
10 *) |
| 25 |
23°542 |
9.42 |
8.03 |
K |
10 |
9.5 |
9.5 |
H_delta |
9.67 |
K |
10 |
9.5 |
9.5 |
H_zeta |
9.67 *) 1) |
| 11 |
23°526 |
9.60 |
9.65 |
» |
7 |
8 |
8 |
» |
7.67 |
» |
8 |
7 |
8 |
» |
7.67 2) |
| 26 |
23°544 |
(9.8) |
9.00 |
» |
10 |
10 |
10 |
» |
10 |
» |
10 |
10 |
10 |
» |
10 *) 3) |
*) According to proper motions by W. L. Elkins,
these stars do not belong to the physical Pleiads.
(Transactions of the Astronomical Observatory of Yale University. Vol. I pg. 356–357)
1) Spectrum ends abruptly just beyond K.
2) Spectrum is fainter than that of 25, but continues much farther into ultraviolet.
3) Spectrum is very faint, ends abruptly just beyond K.
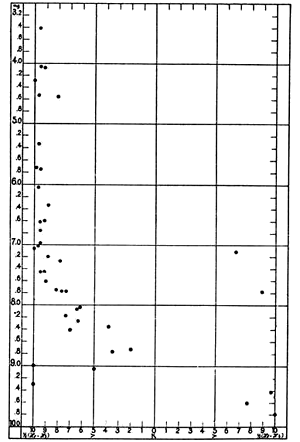 The results from the table are displayed graphically in the figure, to
get a better view. For each star, the mean of comparisons of
K with H_delta and H_zeta is given as the abscissa,
and the photographic brightness as the ordinate.
The results from the table are displayed graphically in the figure, to
get a better view. For each star, the mean of comparisons of
K with H_delta and H_zeta is given as the abscissa,
and the photographic brightness as the ordinate.
From the classification of the spectral types by Miss Maury [4]
follows that even the bright stars in the Pleiades up to 7th magnitude show a
progressive change of the spectral type, from the Maury class V to VII.
That change is apparent mainly in the strength of fainter helium
lines, and is not visible in the small dispersion of the spectra from Göttingen. But the inspection of the figure shows at once that the
progressive change of the spectral type continues up to the stars of 9th
magnitude. From the 7th up to 9th magnitude the K line emerges
stronger and stronger with respect to the hydrogen lines,
what corresponds to the change from the first spectral type to the second.
Only the stars s, 17, 21, 36, 25, 11 and 26 do not fit the sequence; the 21 and 36 are
of earlier spectral type and the other ones of later type than expected from their
brightness. All these stars, with the exception of the star 11 which is just
marginally measurable due to its faintness, belong to those which
have a larger proper motion than the remaining Pleiads, according to
W. L. Elkin. They do not belong to the Pleiades physically.
So it can be said that for the physical Pleiades stars there is
a strict relation between the brightness and the spectral type,
with no exception in the interval from 3th to 9th magnitude.
It should be mentioned that the more pronounced appearance of the K
line by the fainter stars cannot be an artifact due to more or less sufficient
exposure of the spectra, as dependent on the brightness of the stars. There
exists some slight influence of brightness on the comparison of lines, but
experiments with spectra of different exposures show that the influence
is not at all that large (Mr. Hertzsprung will report on this at another
place). By the way, a mere inspection of the character of spectra leads to the same conclusion.
The plausible color differences among the stars in the Pleiades – the fainter the
star, the redder it is – following from the optical and photographic
brightness measurements, are confirmed by the spectral properties. The
color is a function of the radiative properties of the star only.
A selective absorption in the space as an explanation of this effect is evidently inadmissible.
Footnotes
(Click on a footnote number to return to the main text.)
[1] Compare J. G. Hagen: Observations of variable stars. Part I, pg. 4. (Washington 1901)
[2] K. Schwarzschild: Beiträge zur photographischen Photometrie der Gestirne. [Contributions to photographic photometry of stars] Publ. d. v. Kuffnerschen Sternwarte. Bd. V p. 62–63. 1900.
[3] Müller und Kempf: Helligkeit von 96 Plejadesternen. [Brightness of 96 stars in the Pleiades] A. N. 3587–88.
[4] Compare Hertzsprung: Zur Bestimmung der photographischen Sterngröße. [On determination of photographic magnitudes] A. N. 4204 Bd. 176 p. 55.
Göttingen, 1910 June
Hans Rosenberg

 The results from the table are displayed graphically in the figure, to
get a better view. For each star, the mean of comparisons of
K with H_delta and H_zeta is given as the abscissa,
and the photographic brightness as the ordinate.
The results from the table are displayed graphically in the figure, to
get a better view. For each star, the mean of comparisons of
K with H_delta and H_zeta is given as the abscissa,
and the photographic brightness as the ordinate.