Úvodní stránka > Capella: Jak se váží hvězdy?

Capella: Jak se váží hvězdy?

Pokud je po ruce vše potřebné, pak stejně snadno jako třeba jablka. Ostatně přesvědčte se o tom sami. Capella (α Aurigae) je v tomto směru doslova učebnicový příklad. Potřebovat budeme jenom dva obrázky (pdf, 62 kB) převzaté z práce D. J. Barlowa a jeho kolegů (PASP, 105, 476, 1993), pravítko a obyčejnou kalkulačku. Capella je vhodná proto, že v jejím spektru jsou zřetelné absorpční čáry obou hvězd, oběžné dráhy jsou přesně kruhové a vzájemné polohy složek jsou důkladně proměřené interferometricky. První graf ukazuje křivky radiálních rychlostí - plné symboly odpovídají obru třídy G8 III, prázdné pak druhé složce, obru G1 III. Obě křivky jsou čistými sinusoidami. S pomocí stupnice na svislé ose, cejchované v kilometrech za sekundu, není problémem určit jejich amplitudy K₁ a K₂. Poměr těchto amplitud je zároveň převráceným poměrem hmotností složek.

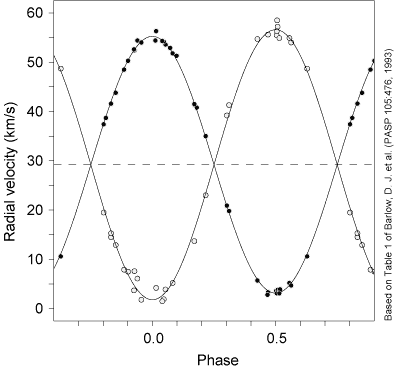
Vlevo: Křivky radiálních rychlostí složek Capelly jsou dokonalé sinusoidy, což svědčí o tom, že jejich dráhy jsou kruhové. Upraveno z práce D.J. Barlowa, F.C. Fekela a C.D. Scarfeho (PASP 105, 476, 1993). Na základě měření uskutečněnýczh autory na McDonald Observatory a KPNO s použitím starších dat z Dominion Astrophysical Observatory (Batten aj., PASP 103, 623, 1991)

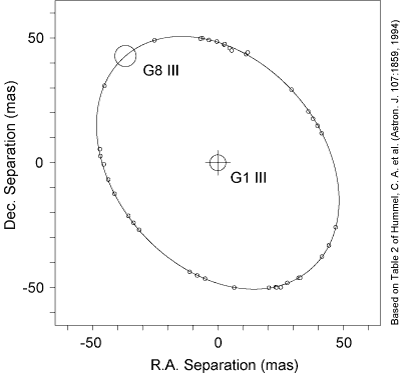
Vpravo: Zbývající ingredience nutná pro zvážení Capelly je její dráha (přesněji trajektorie) změřená interferometrem Mark III (umístěný na Mt. Wilsonu nedaleko Los Angeles, provozovaný Naval Research Laboratory s finančním přispěním Office of Naval Research). Upraveno z práce Hummel aj., Astron. J. 107, 1859, 1994.

Pokud bychom se na oběžnou rovinu dívali z boku (sklon i = 90°), pak by se amplitudy navíc rovnaly oběžným rychlostem v₁ a v₂ složek okolo těžiště dvojhvězdy. Pro obecný sklon oběžné roviny platí

v₁ = K₁/sin i

(a obdobně pro druhou hvězdu). U většiny dvojčarových spektroskopických dvojhvězd sklon neznáme a ve výsledku se pak musíme spokojit s dolní mezí pro hmotnost složek. Výjimkou jsou zákrytové dvojice, kde je sklon blízký k 90° a lze jej přesně určit analýzou světelné křivky. Capella naštěstí nabízí jinou možnost: využít interferometrických měření. Na druhém obrázku je pozorovaná dráha jedné hvězdy vůči druhé (všimněte si přesnosti měření - jeden dílek na okraji grafu odpovídá 0,002”!). Poměr kratší a delší osy této krásné elipsy je roven cos i.

Teď už máme pravé oběžné rychlosti a stačí je vynásobit délkou oběžné periody P, která je 104,0233 dne. Tak dostaneme obvody a tím i poloměry oběžných drah r₁ a r₂ vzhledem k těžišti. Jejich součet je roven velké poloose a, kterou můžeme dosadit do vztahu pro třetí Keplerův zákon a dostaneme celkovou hmotnost dvojhvězdy. Platí

M₁ + M₂ = 4π²a³/P²G.

Musíme jen dát pozor, abychom dosazovali poloosu v metrech a periodu v sekundách. Hodnota gravitační konstanty G v jednotkách SI je 6,672×10^-11. Celková hmotnost Capelly tak vyjde v kilogramech. Pro přepočtení na běžnější jednotku stačí znát hmotnost Slunce, 1,989×10³⁰ kg.

Nakonec zbývá spočítat hmotnosti jednotlivých složek, známe-li jejich poměr a součet, ovšem to už jsou opravdu kupecké počty. Výsledek stojí za to. Pokud budeme pracovat pečlivě, dostaneme správné hodnoty s přesností pouhých několika procent. A to nemluvím o tom, že z obou obrázků je možné jednoduše spočítat i vzdálenost Capelly od nás. Ale to určitě zvládnete sami.